Построение модели
- Методология /
-
8475
Клинико-экономическое моделирование – это многофакторный математический метод, используемый в экономической оценке ЛП и позволяющий оценить эффективность и затраты за определённый временной горизонт при применении сравниваемых лекарственных препаратов.
Преимуществом моделирования является не только анализ рассматриваемой проблемы с различных сторон, но и возможность прогнозирования развития события при недостаточности исходных клинических данных [1].
Технические возможности модели определяются целями и задачами проводимого клинико-экономического исследования или анализа влияния на бюджет.
Базовыми типами моделей являются: модель «дерево решений», модель Маркова, смешанная (гибридная) модель.
Прежде чем приступить к построению модели, следует определиться с базовой структурой моделирования, которая существенно влияет на результаты [2]:
- позиция исследования;
- препараты сравнения;
- временной горизонт;
- тип модели;
- наличие релевантных данных для определения значений входных параметров.
В процессе моделирования можно выделить следующие этапы [3]:
- Разработка дизайна модели. Необходимо выбрать вид, структуру и параметры модели для анализа результатов и оценки достижения заданной точности моделирования с последующим выбором критериев оценки эффективности и безопасности в зависимости от заданной нозологии.
- Графическое изображение. Необходимо создать графическое изображение модели с помощью Edraw Max Pro, TreeАge Рro или других программ.
- Интеграция методов экономического анализа. Необходимо внедрить в модель такие фармакоэкономические методы, как анализ «затраты-эффективность» или анализ «затраты-полезность» и анализ влияния на бюджет, использовать дисконтирование затрат при временном горизонте модели более одного года, а также анализ чувствительности полученных результатов.
- Получение результатов в модели. Необходимо ввести различные исходные данные в разработанную модель, получить результаты различных сценариев, определить доминирующий ЛП или инкрементальный показатель соотношения затрат и эффективности (ICER), оценить его относительно либо референтного ICER (включённого в соответствующие ограничительные перечни), либо «порога готовности платить», выявить возможные ошибки или отклонения в модели.
- Оценка устойчивости. Необходимо провести оценку устойчивости полученных результатов к изменениям таких входных параметров, как стоимость препаратов сравнения и их эффективность.
Для цели подачи Предложения на включение в Перечни, как правило, необходимы аналитические модели принятия решений (АМПР), разработанные на базе программ обработки электронных таблиц MS Excel, которые обладают широкими функциональными возможностями и позволяют провести различные виды клинико-экономического анализа и анализа влияния на бюджет, включив в расчёт различные входные параметры и влияющие факторы [3].
Другой тип модели – это CORE-модели (англ. cost outcome research effectiveness). Главным отличием CORE-моделей от АМПР является более сложный анализ эффективности оцениваемых ЛП, учитывающий множество факторов. CORE-модели, как правило, разрабатываются на международном уровне, однако проблемы с адаптацией к условиям российской системы здравоохранения ограничивают их применение. Также они являются наиболее дорогостоящими при разработке. Помимо этого, именно для CORE-моделей наиболее характерна проблема «чёрного ящика», так как в большинстве случаев процесс вычислений модели недоступен для пользователя или они построены по облачному типу (вычисления производятся на удалённом сервере) [3].
Основные принципы построения модели
Прежде чем приступить к построению модели, следует поставить перед собой конкретные цели, иначе вы рискуете создать модель, которая не будет соответствовать стоящей перед вами задаче. Составьте список данных, которые необходимо определить с её помощью. Скорее всего, вы хотите проверить гипотезу, предсказать исходы и затраты на их лечение, а также провести анализ «затраты-эффективность» и анализ влияния на бюджет.
Посмотрите, что уже было сделано другими: не надо изобретать велосипед. Может, кто-то уже создал модель, которая подходит для вас. При этом следует убедиться в том, что готовую модель можно использовать в вашем случае.
Хорошая модель должна быть максимально простой, чётко описанной, отражать ключевые клинические характеристики процесса заболевания и рассматриваемых методов лечения, использовать для входных данных наилучшую доступную информацию (РКИ, систематические обзоры и метаанализы), а также учитывать неопределённость в отношении входных данных и допущений модели.
Определите, что вам известно, какими исходными данными по эпидемиологии, эффективности и безопасности вы располагаете. Отметьте, какие данные имеют первоочередное значение, а какие не столь важны. Построение модели основано на доступных данных из ранее проведённого вами информационного поиска. В случае отсутствия некоторых данных оценивается приемлемость использования собственно моделирования недостающих данных (например, на экстраполяции данных или экспертном мнении) и рассматривается адекватность принимаемых в связи с этим допущений.
После информационного поиска приступают к описанию и реализации сценариев модели. Под сценарием модели понимается логически завершённый и математически независимо описанный (от других расчётов) путь в модели от вводных данных до выходных результатов [3].
Изобразите модель в виде схемы (см. пример на рис. 1), которая поможет вам разобраться, как именно работает ваша модель. Обязательно включите в схему исходные данные – это поможет вам при дальнейшей разработке модели.
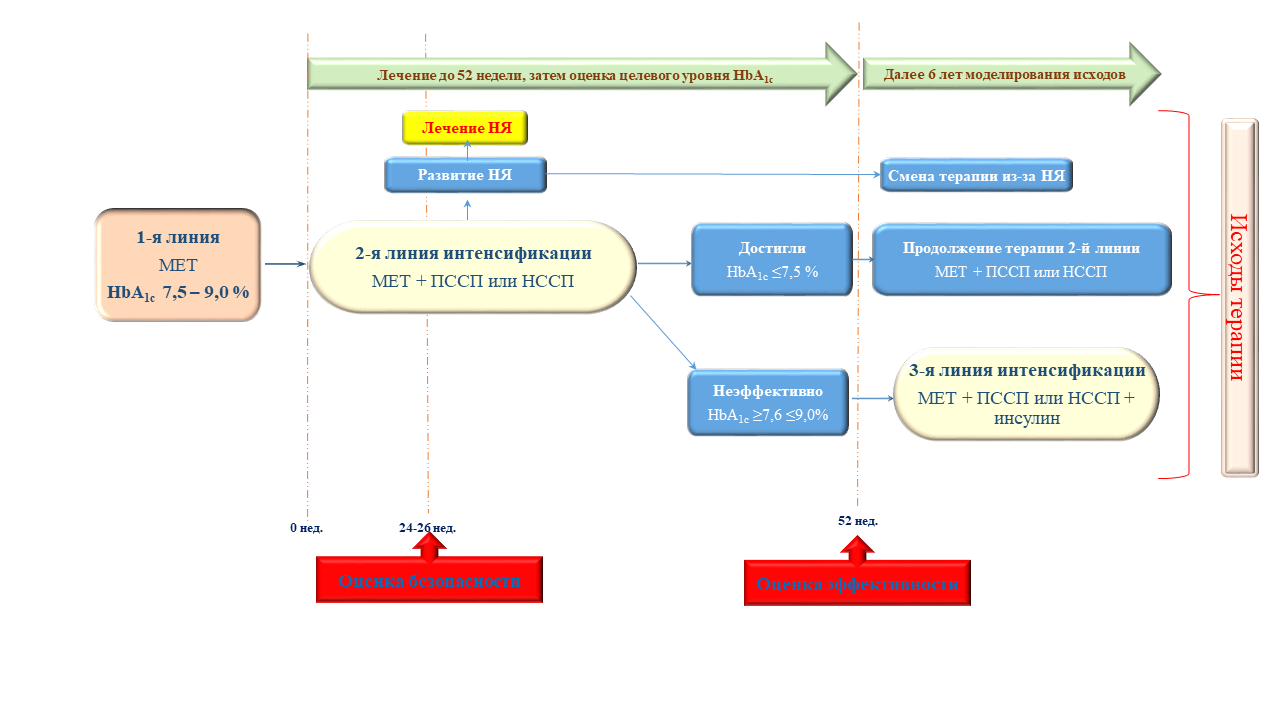
Рис. 1. Пример схемы модели терапии сахарного диабета второго типа при неэффективности метформина [4]
Примечания: МЕТ – метформин; ПССП – пероральные сахароснижающие препараты; НССП – неинсулиновые сахароснижающие препараты; НЯ – нежелательные явления.
Отражая последствия внедрения того или иного ЛП, фактически, модель описывает определённый участок маршрута (или весь) пациента, связанного с применением оцениваемого ЛП. При этом маршрут пациента в рамках модели имеет две обязательные точки: точка входа пациента в модель и точка выхода пациента из модели (исходы с оценкой результата на выходе); при необходимости в модели могут отражаться дополнительно промежуточные этапы между указанными обязательными точками. Принимая во внимание, что маршрут пациента зависит от характеристики пациента, условий оказания медицинской помощи и других влияющих факторов, одна модель может иметь как один сценарий, так и несколько сценариев [3].
После стадии предварительной подготовки и планирования следует приступить к построению самой модели. Используйте при этом созданную ранее схему, исходные данные и другую полезную информацию. Чаще проверяйте свои действия, чтобы не допустить ошибку. Убедитесь в том, что ваша модель действительно описывает наблюдаемые соотношения между данными величинами и процессами [5].
Маршрут пациента в моделях наиболее часто описывается (или отслеживается) с использованием трёх подходов к моделированию: модели «дерева решений» и модели Маркова или их комбинации (гибридной модели). Главное различие между указанными подходами заключается в том, что модель «дерева решений» рассматривает состояние пациентов, как правило, только на входе в модель и на выходе (выход при этом может быть представлен набором конечных состояний), таким образом фактор времени в модели игнорируется [3] (см. рис. 2).
Конечное состояние в модели «дерева решений» определяется суммой заданных последовательно развивающихся событий, которые случаются с пациентом на протяжении движения по маршруту с определённой вероятностью. Наличие в модели параметров вероятности отражает её прогностический характер [3].
Модель Маркова, в свою очередь, позволяет анализировать движение пациента на всём протяжении маршрута, благодаря наличию так называемых марковских состояний – это фиксированные состояния, в которых может пребывать пациент, характеристики которых известны (см. рис. 3). В этом случае состояние пациентов на выходе из модели определяется как сумма характеристик марковских состояний, в которых пребывали пациенты за рассматриваемый в модели временной горизонт. Из этого следует, что модель Маркова, в отличие от модели «дерево решений», учитывает временной фактор. Поэтому марковские модели обладают большей точностью в сравнении с моделями «дерева решений», однако являются более сложными в исполнении и требуют большего массива исходных данных [3].
Согласно существующей практике использование моделей «дерево решений» считается целесообразным при клинико-экономическом исследовании остропротекающих заболеваний, продолжительность которых невелика (короткий временной горизонт модели), что позволяет нивелировать фактор игнорирования времени в данном типе моделей [3].
Марковские модели рекомендуется использовать при клинико-экономических исследованиях хронических заболеваний или заболеваний, характеризующихся выраженной стадийностью, однако главным условием для реализации модели Маркова является доступность данных о значениях марковских переходов [3].
Возможна комбинация подходов «дерева решений» и марковского моделирования, так называемая гибридная модель, когда, например, вход пациентов в модель до некоторого промежуточного этапа описывается посредством модели «дерево решений», после чего пациенты переходят в модель Маркова со всеми характерными для неё атрибутами: марковскими состояниями, марковскими циклами и переходами (см. рис. 4) [3].
Далее определите формулы, которые понадобятся вам для решения поставленной задачи. Необходимо ясно представлять себе, как именно вы будете подставлять исходные данные в имеющиеся формулы, посредством которых на основе вводных данных рассчитываются результаты.
Объём и сложность математического аппарата определяется количеством учитываемых в модели факторов (вводных данных), сценариев и реализуемых в модели методов клинико-экономического анализа, наличием дисконтирования, анализа чувствительности и т. п. [6].
Также в контексте математического описания клинико-экономических моделей можно выделить детерминированные и стохастические модели. Первые характеризуются использованием дискретных данных – заданных численных значений, тогда как в стохастических моделях вычисления производятся на основе заданных параметров распределений тех или иных величин (вводных данных). При этом результатом детерминированных моделей являются точечные оценки, в то время как стохастические модели позволяют произвести интервальную оценку в форме области возможных значений, каждое из которых имеет свою вероятность наступления. Таким образом, стохастические модели более эффективно реализуют прогностическую функцию, демонстрируя все возможные результаты в соответствии с заданными распределениями значимых оцениваемых параметров [6].
Каждый раздел модели в MS Excel должен быть чётко структурирован по типу представляемой информации и иметь общую информацию, листы c вводными ячейками, листы с результатами моделирования и справочной базы с приложениями (см. табл. 1).
Таблица 1. Формат модели в MS Excel и содержание
|
Лист/листы в MS Excel |
Содержание |
|
Титульный лист |
Название модели, версия, дата, исполнители |
|
Общая информация
|
· Цель исследования · Дизайн исследования · Используемые методы анализа · Сравниваемые стратегии терапии · Численность целевой популяции · Точка зрения · Временной горизонт · Источники данных об эффективности и безопасности |
|
Структура модели |
· Описание структуры модели · Представление обобщённой схемы модели (графическое изображение) · Описание основных допущений модели с их обоснованием · Ограничения модели |
|
Ключевые параметры модели |
Указание перечня всех ключевых параметров, использованных в расчётах, с приведением их значений и источников информации для каждого значения, таких как: · Исходные данные (пол, возраст, заболеваемость, смертность и прочее) · Стоимости (затраты): - Препараты сравнения - Альтернативные медицинские вмешательства - Медицинские услуги · Показатели эффективности · Показатели безопасности · Показатели полезности · Вероятность исходов |
|
Расчёты |
Приведение расчётов (формул) для всех затрат, которые учитываются в исследовании |
|
Результаты
|
· Смоделированные исходы лечения · Прямые медицинские затраты · Анализ «затраты-эффективность» · Анализ влияния на бюджет · Дисконтирование |
|
Анализ чувствительности |
· Результаты анализа чувствительности при изменении исходных параметров модели |
|
Прочее |
· Источники информации и приложения |
|
Примечание: всем таблицам и графикам в модели должны быть присвоены название и номер [7] |
|
Важнейшим достоинством моделирования является возможность оценки влияния вариабельности исходных параметров на результаты (настройка модели). Следует помнить, что все клинические исследования проводятся на ограниченных по размеру группах. Затем характеристики выборки переносятся на популяцию путём расчёта доверительных интервалов, при этом оценить влияние колебаний показателей в пределах доверительного интервала на результаты клинико-экономического анализа можно только в модели.
Моделирование также даёт возможность оценивать влияние ошибок, связанных не только с размером выборки, но и с другими факторами. Например, в исследовании учитывались больные с сопутствующей патологией в размере 5 % от общего числа пациентов. Предположим, что в реальной клинической практике таких больных может быть 10–15 %. Что будет с выявленными закономерностями, если в качестве входного параметра вместо 5 % мы укажем 10 % таких больных?
Источниками неопределённости при моделировании могут быть:
- выбранная структура модели (данный вид неопределённости связан с видом используемой модели для экономической оценки: выбор типа модели, выбор состояний при использовании модели Маркова, экстраполяции исходов после окончания периода наблюдения, длительность марковского цикла и т. д.);
- неопределённость значений входных параметров (такого рода неопределённости связаны с ошибками измерений, разбросами значений внутри выборок и т. д.);
- неопределённость при выборе методологии исследования (в данном случае рассматриваются неопределённости, связанные с методологией учёта затрат, выбором временного горизонта моделирования, ставки дисконтирования и т. д.).
Заключительным этапом разработки клинико-экономической модели является её валидация для оценки адекватности отражения в модели описываемого объекта и получаемых выводов по отношению к действительности [3]. Проверьте правильность модели, прежде чем её использовать. Подставьте численные данные и посмотрите, получатся ли ожидаемые результаты. Имеют ли они смысл? Повторите свои действия, чтобы убедиться, что получаются воспроизводимые результаты.
Прежде чем использовать модель в дальнейшем, подумайте над тем, как её можно улучшить. Существуют ли дополнительные факторы, которые следует учесть? Обладает ли модель ограничениями, которых можно избежать? Не исключено, что вам удастся улучшить свою модель и она станет более пригодной для дальнейшего применения.
Модель «дерево решений»
Модель «дерево решений» (англ. decision tree model) – это способ математического моделирования, при котором процесс лечения представляется в виде диаграммы, иллюстрирующей вероятность каждого из исходов, а также его стоимости применительно к конкретной ситуации, при этом не учитывается временной фактор [3].
Модель «дерево решений» обычно используется для описания процесса лечения острого заболевания. Построение данной модели возможно при условии анализа нескольких ЛП с различной и известной вероятностью исходов, при аналогичности измеряемых показателей. Таким образом, основные условия для построения «дерева решений» следующие:
- есть два (или более) альтернативных варианта с различной вероятностью исходов;
- известна вероятность наступления каждого из исходов;
- известна или возможно рассчитать стоимость каждого исхода.
Моделирование на основе «дерева решений» можно условно разделить на несколько этапов:
- рисуем диаграмму «дерева решений»;
- ставим вероятности исходов;
- оцениваем исходы в денежном выражении;
- анализируем результаты;
- проводим анализ чувствительности полученных результатов.
Диаграмма «дерева решений» представляет собой разветвлённую структуру. Рисуют деревья слева направо (см. рис. 1). Ветви «дерева решений», которые сами по себе обозначают выбор конкретного ЛП или же отмены из-за развития НЯ, излечения, отказа от терапии из-за некомплаентности и прочего, могут относиться к первому, второму, третьему и последующим порядкам [3].
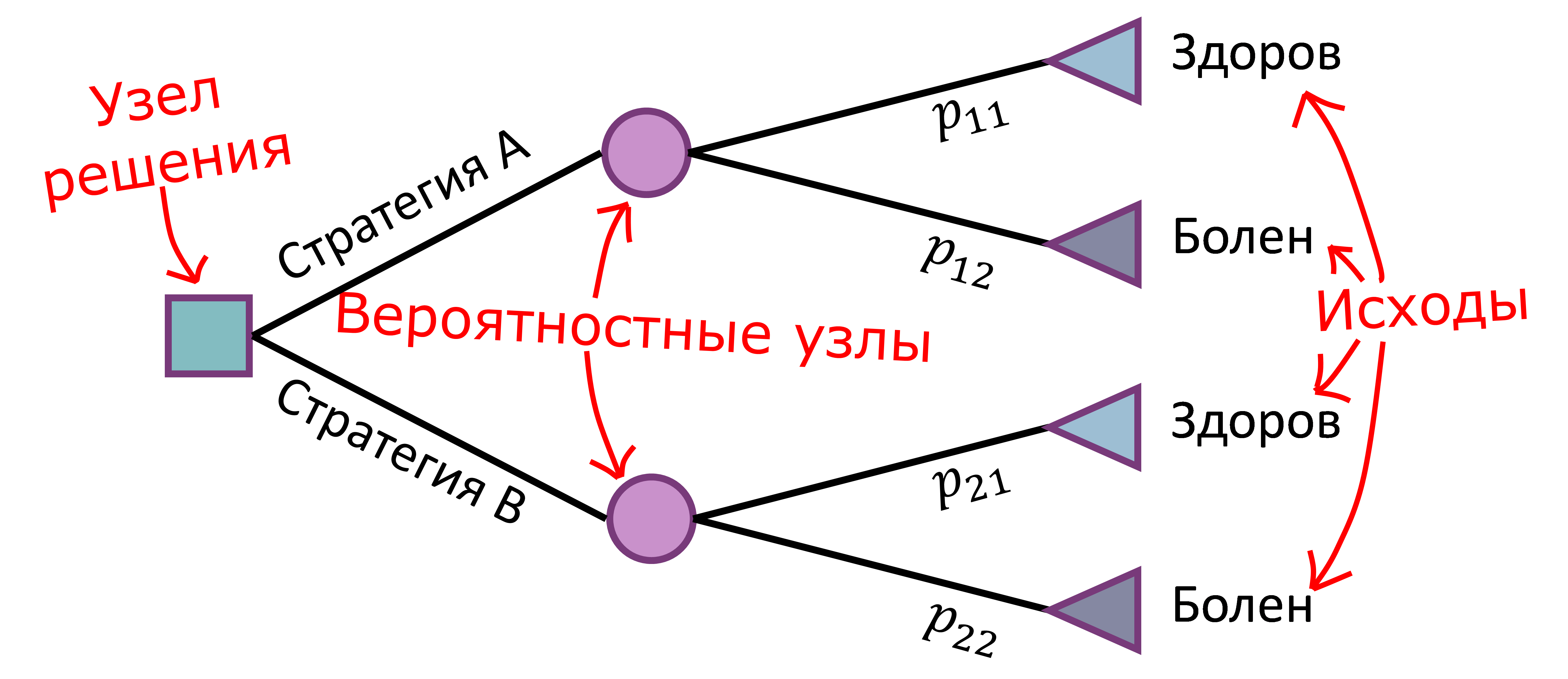
Рис. 1. Пример модели «дерево решений»
Каждая ветвь «дерева решений» заканчивается клинически значимым с точки зрения исследователя исходом, например выздоровлением, улучшением клинических показателей, смертью. Места разветвлений, называемые узлами решений, представляют собой точки, в которых могут произойти разные события, и соответствуют моментам времени, когда происходит принятие решений или выбор альтернатив. При графическом представлении модели такие узлы принято изображать квадратами.
Вероятностные узлы соответствуют моментам времени, когда наступает случайное событие с тем или иным результатом. Ветви, исходящие из вероятностных узлов, представляют собой возможные исходы, которые наступают с заданной вероятностью (p). Вероятности каждого клинического исхода исчисляются от 0 до 1, в результате чего сумма вероятностей ветвей каждого порядка должна составлять единицу. При графическом представлении модели такие узлы принято изображать кружочками.
Далее рассчитываются затраты альтернативных схем терапии путём последовательного перемножения значения вероятностей по каждой ветви справа налево и последующего умножения полученного итогового значения вероятности на стоимость исхода, представленного в конце ветви [3].
С клинической точки зрения ветви «дерева решений» заканчиваются возможными исходами заболевания или промежуточными результативными показателями, в качестве которых может выступать смерть, улучшение клинических показателей или выздоровление, переход острого заболевания в хроническую форму и так далее, хотя вместо них могут быть представлены и другие исходы – продолжительность и качество жизни.
Терминальные узлы соответствуют конечным состояниям, связанным с соответствующей ветвью дерева. Понятно, что анализ всегда ограничен временным горизонтом моделирования. Помимо смерти, результаты, выбранные терминальными (конечными) точками дерева, могут не быть истинными конечными результатами, а быть просто удобной точкой для дальнейшего анализа. Таким образом, каждое дерево может содержать терминальные узлы, которые представляют дальнейший прогноз для конкретной комбинации последующих характеристик и событий. Графическим знаком изображения конечных состояний является треугольник.
Каждый проход по определённым ветвям дерева определяет потенциальный исход. Для каждого вероятностного узла указываются значения вероятностей наступления событий. В конце каждой ветви справа указываются итоговые затраты для каждой из стратегий лечения (ветви «дерева решений») и значения выбранных критериев эффективности. Для каждой стратегии вычисляются средние затраты и итоговые показатели эффективности.
С учётом того, что в период исследуемого заболевания события могут повторяться, количество ветвей в модели будет с каждым разом увеличиваться, достигая нескольких десятков, делая модель «дерево решений» очень объёмной, что может впоследствии привести к неточности и ошибкам в модели. В этом случае лучше использовать модель Маркова, отличающуюся наибольшей эластичностью в сравнении с «деревом решений» [3].
Модель Маркова
Клинико-экономические исследования, изучающие применение ЛП, снижающих заболеваемость и смертность от хронических заболеваний, лучше всего оценивать с использованием марковских моделей.
Модель Маркова (англ. Markov model) представляет собой математическую модель, которая строится из состояний и вероятностей перехода из одного состояния в другое в течение определённого временного горизонта, и определяет особенности течения и исходов заболевания, используя клинические данные популяции больных [3].
Применение модели Маркова целесообразно в тех случаях, когда болезнь можно разделить на ряд последовательных фаз (например, исходное состояние – полное здоровье, конечное – смерть пациента, промежуточные – стадии заболевания или же этапы диагностики или лечения).
Основными характеристиками для модели Маркова являются: возможные состояния пациента; вероятности перехода от одного состояния к другому; фиксированный период, или цикл, внутри которого применяется вероятность перехода [3].
Модель Маркова используют для:
- описания долгосрочного развития хронических заболеваний, при наличии данных только за ограниченный период;
- прогнозирования будущих затрат и исходов;
- экстраполяции краткосрочных (клинических) результатов на долгосрочные экономические оценки здоровья.
Марковское моделирование позволяет исследователям моделировать изменения в развитии заболевания на протяжении времени, относя субъектов в различные состояния здоровья по мере того, как они стареют. В марковской модели люди наблюдаются вначале в одном временном интервале, а затем в другом временном интервале (например, первый год, а затем второй год). По мере того, как человек стареет, модель анализирует изменения в состоянии его здоровья: некоторые люди умирают, в то время как у других развивается заболевание. Когда у человека развивается какое-то заболевание, это приводит к тому, что он (или она) генерирует расходы (затраты), связанные с этим состоянием, и происходят изменения в HRQoL. Все эти события описываются в марковской модели с использованием марковских состояний, то есть определённого состояния здоровья [6].
На рис. 2 представлено графическое изображение модели Маркова с тремя состояниями: «здоровье», «болезнь», «смерть». Каждое состояние является постоянным на протяжении фиксированного интервала времени [6]. Для каждого состояния известна вероятность перехода из одного состояния в другое на протяжении определённого временного периода. Стрелки указывают на допустимые переходы. При этом каждому состоянию соответствуют определённые затраты и эффекты.
Временной интервал исследования разделяется на равные отрезки времени, которые называются марковскими циклами. Продолжительность циклов Маркова выбирается таким образом, чтобы каждый из них представлял собой минимально короткий промежуток времени, имеющий в процессе лечения определённое существенное значение. Обычно в экономическом анализе марковский цикл принимается за 1 год, 6, 3 или 1 месяц, исходя из характеристики заболевания [3].
При большой продолжительности цикла Маркова рекомендуют учитывать коррекцию полуцикла (англ. half-cycle correction), то есть допущение наступления события в середине цикла, что может повлиять на итоговые суммарные затраты рассматриваемых стратегий [8].
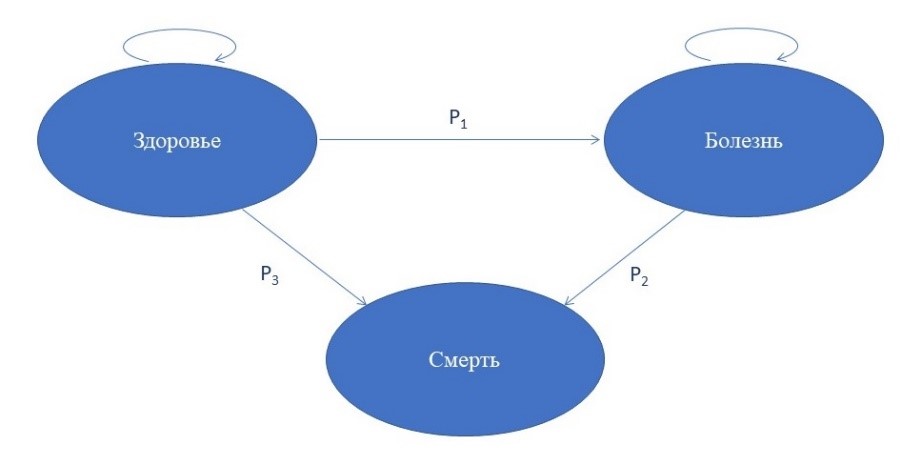
Рис. 2. Пример модели Маркова
Примечание: Р – вероятность перехода из одного состояния в другое.
Для того чтобы марковский цикл прекратился, в нём должно присутствовать по крайней мере одно состояние, выйти из которого пациент не сможет. Так как после прохождения достаточного количества циклов вся изучаемая популяция пациентов переходит в замкнутое состояние, подобное состояние именуется абсорбирующим. Из состояния абсорбции невозможен переход в другое состояние. Наиболее часто использующимся абсорбирующим состоянием является смерть пациента (клинический (основной) исход). При этом временной горизонт в модели Маркова может быть конкретным (например, 10 лет) или соответствовать всей жизни пациента, то есть учитывается с цикла 0 до момента, когда все моделируемые пациенты умрут [3].
В модели Маркова исследуется когорта пациентов, которая находится в начальном состоянии (например, состояние «здоров» или «без прогрессирования») до исследования и распределяется в разные состояния через каждый цикл. В конце каждого цикла с помощью вероятностей перехода P(t) из одного состояния в другое рассчитывается количество пациентов, находящихся в определённом состоянии, что позволяет оценить затраты и эффективность терапии для каждой исследуемой стратегии. При этом необходимо отметить, что количество пациентов в когорте во всех циклах не меняется и не отличается от первоначального значения. Например, если когорта состоит из 100 пациентов, то во всех циклах количество пациентов должно составлять 100 [3]. В модели с количеством состояний N возможно N*N переходов, однако в реальности не все переходы возможны. При этом возможны два варианта моделирования: вероятности переходов могут быть постоянны или меняться во времени. Так, при длительном горизонте моделирования возможно рассмотрение вероятности смерти в зависимости от возраста.
Обычным методом представления марковских моделей является дерево марковских циклов, каждое состояние отображается на нём в виде ответвления от марковского узла. Марковский процесс обычно представляется в виде диаграммы перехода состояний [3].
Набор всех вероятностей перехода из одних состояний в другие называется матрицей вероятностей переходов и обычно представляется в виде таблицы (см. табл. 2), где в строках стоят исходные состояния, а в столбцах состояния, в которые может попасть пациент к концу цикла.
Таблица 2. Матрица фиксированной вероятности перехода из состояния в состояние
|
Исходные состояния (переходы из): |
Вероятность перехода в состояние: |
|||
|
Здоровье |
Болезнь |
Смерть |
Итого |
|
|
Здоровье |
0,7 |
0,2 |
0,1 |
1 |
|
Болезнь |
0,0 |
0,6 |
0,4 |
1 |
|
Смерть |
0,0 |
0,0 |
1,0 |
1 |
С технической точки зрения модель сводится к последовательному перемножению матриц вероятностей и оценке на каждом этапе смоделированной численности пациентов в каждом состоянии с учётом времени развития состояния в цикле (см. табл. 3). Данная табл. 3 представляет собой пример матрицы вероятностей переходов для марковской модели, состоящей из трёх состояний. Столбцы показывают переходы между состояниями, которые возможны в рамках одного цикла. Сумма вероятностей в строке должна равняться единице. Нулевая вероятность показывает, что в данной модели такой переход невозможен.
Таблица 3. Матрица вероятности перехода из состояния в состояние, зависящей от времени
|
Исходные состояния (переходы из): |
Вероятность перехода в состояние: |
|||
|
Здоровье |
Болезнь |
Смерть |
Итого |
|
|
Здоровье |
1-P(t)-0,1 |
P(t) |
0,1 |
1 |
|
Болезнь |
0,0 |
0,6 |
0,4 |
1 |
|
Смерть |
0,0 |
0,0 |
1,0 |
1 |
|
Временная зависимость вероятности перехода |
||||
|
Марковский цикл (t), год, мес. и пр. |
1 |
2 |
3 |
4 |
|
Вероятность перехода в марковском цикле, P(t) |
0,23 |
0,28 |
0,33 |
0,41 |
Таким образом, через определённый промежуток времени (марковский цикл) возможен переход из одного состояния в другое с определённой вероятностью, которая может оставаться постоянной или меняться на протяжении анализа и определяться на основании результатов клинических или эпидемиологических исследований по следующей формуле [3]:
P(t)=1-e(-rt), где
P(t) – вероятность перехода в марковском цикле;
r – относительный риск перехода в состояние;
t – марковский цикл (временной интервал);
е – основание натурального логарифма (математическая константа, иррациональное и трансцендентное число; приблизительно равно 2,71828).
При применении модели Маркова существуют некоторые ограничения (марковские допущения). Во-первых, переход от состояния к состоянию осуществляется только в конце цикла, что может впоследствии приводить к субъективной оценке. Во-вторых, модель Маркова не сохраняет данных о событиях на более ранних циклах исследования, то есть в конце цикла описывает количество пациентов в каждом из исследуемых состояний (другими словами, марковская модель не имеет памяти (англ. memoryless property)) [3].
При проведении клинико-экономического исследования на основе модели Маркова следует придерживаться следующего алгоритма действий:
- определить состояния и переходы;
- выбрать длину цикла;
- определить множество вероятностей перехода между состояниями;
- присвоить каждому состоянию здоровья соответствующие стоимости и полезности;
- определить первоначальное распределение целевой популяции;
- провести расчёты;
- оценить результаты.
Гибридная модель
Часто при проведении клинико-экономического анализа используется смешанный тип моделей, так называемая гибридная модель, состоящая из «дерева решений», внутри которого в определённых узлах используется марковская модель. Пример такой модели изображён на рис. 3.
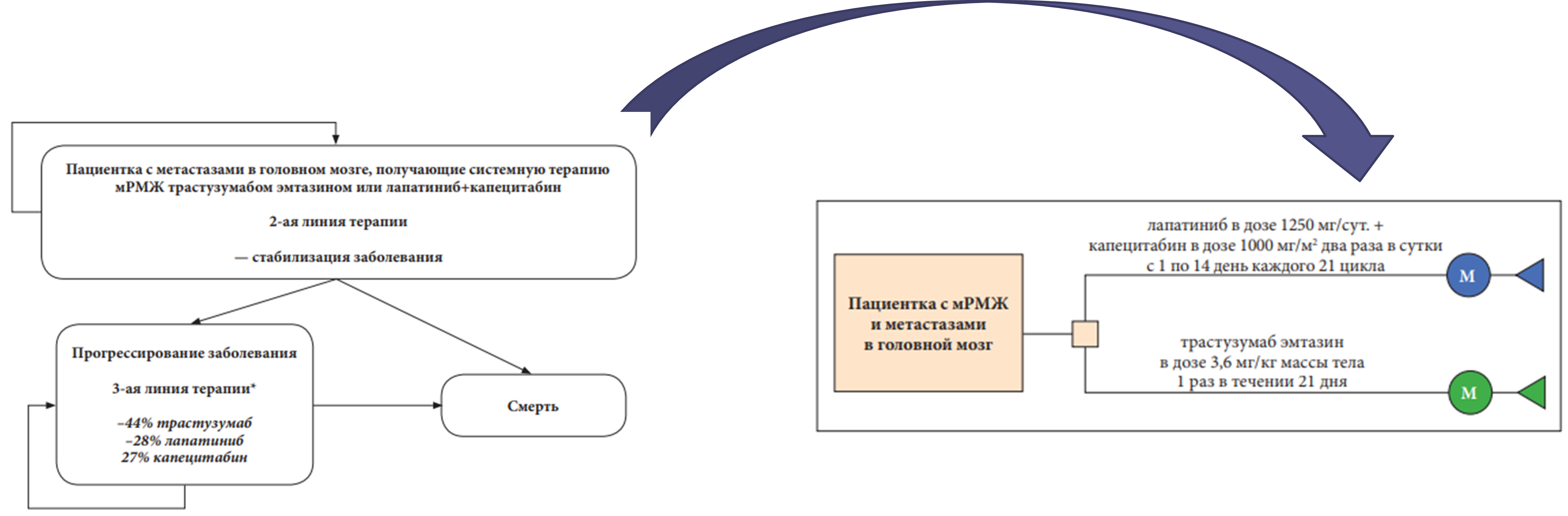
Рис. 3. Пример гибридной модели [9]
Другие методы моделирования
При проведении клинико-экономического исследования возможно использование дополнительных методов моделирования, таких как когортное моделирование, дискретно-событийное моделирование и прочие [3].
При когортном моделировании вся группа (пере)распределяется по состояниям после каждого цикла (все пациенты одновременно) (см. рис. 4). В начале моделирования все пациенты находятся в состоянии «Здоровье». Вероятность переходов определяет распределение пациентов по трём различным состояниям во втором и последующих циклах. В конце каждого цикла, для определения состояния, в которое перейдёт объект, используется генератор случайных чисел вместе с вероятностями перехода.
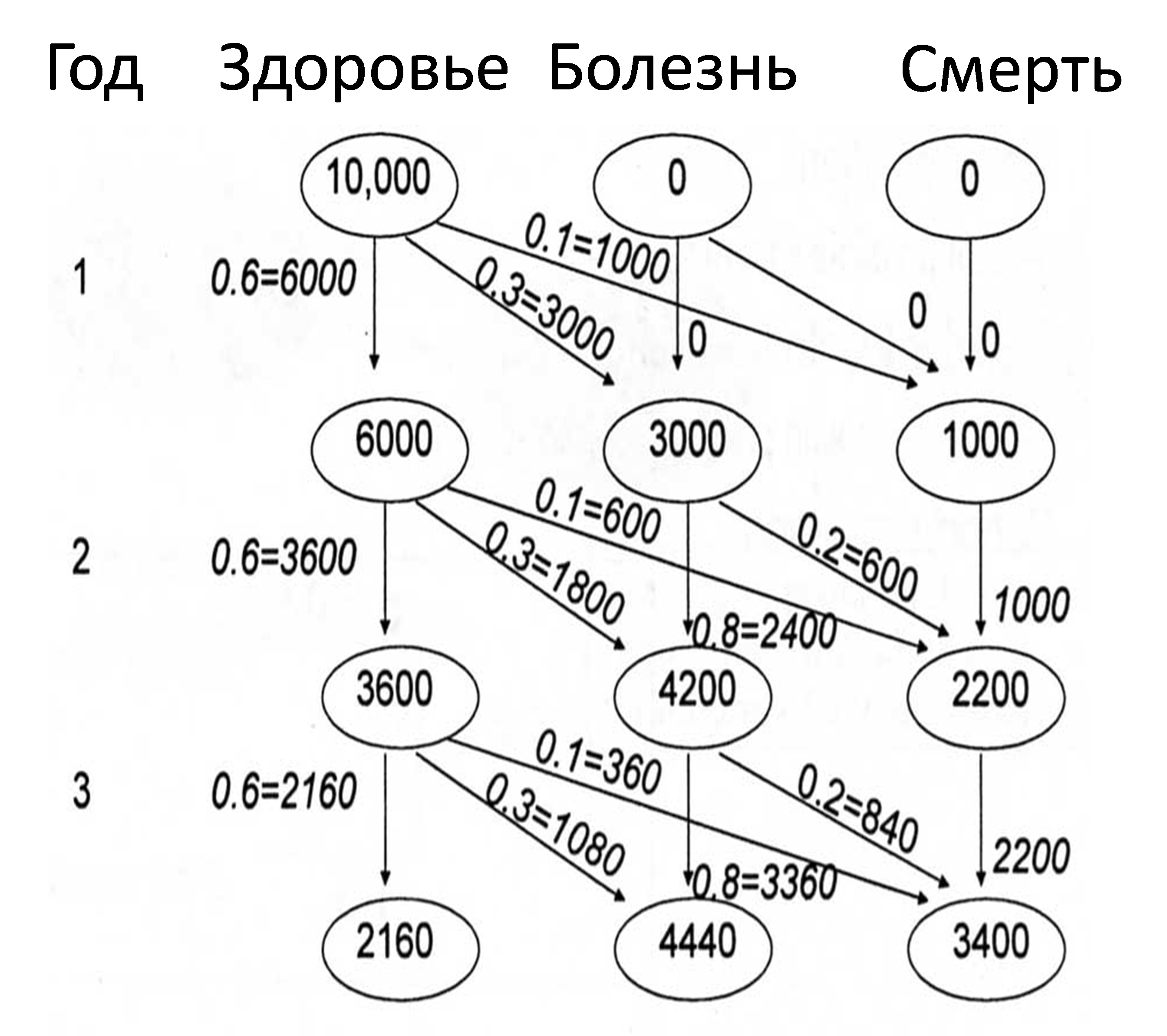
Рис. 4. Пример когортного моделирования
Рассмотрим пример подсчёта затрат с использованием когортной симуляции. Для удобства, расчёты проводились на 1000 пациентов, при этом целью являлось оценить возможные затраты на одного пациента после 10 марковских циклов. Для этого необходимо определить стоимость каждого состояния. Предположим, что затраты, соответствующие состояниям «Здоровье» и «Смерть», равны нулю, а состоянию «Болезнь» – 100 руб. Суммарные затраты рассчитываются исходя из количества циклов и количества пациентов, находящихся в каждом из состояний. Средние затраты на одного пациента рассчитываются путём деления суммарных затрат на количество пациентов в модели (см. табл. 4).
Таблица 4. Пример подсчёта затрат с использованием когортной симуляции
|
Цикл |
Здоровье |
Болезнь |
Смерть |
Затраты (руб.) |
|
|
На цикл |
Кумулятивные |
||||
|
0 |
1000 |
0 |
0 |
0 |
0 |
|
1 |
600 |
300 |
100 |
30 000 |
30 000 |
|
2 |
360 |
420 |
220 |
42 000 |
72 000 |
|
3 |
216 |
444 |
340 |
44 400 |
116 400 |
|
4 |
130 |
420 |
450 |
42 000 |
158 400 |
|
5 |
78 |
375 |
547 |
37 488 |
195 888 |
|
6 |
47 |
323 |
630 |
32 323 |
228 211 |
|
7 |
28 |
273 |
699 |
27 258 |
255 469 |
|
8 |
17 |
226 |
757 |
22 646 |
278 116 |
|
9 |
10 |
186 |
804 |
18 621 |
296 737 |
|
10 |
6 |
152 |
842 |
15 199 |
311 936 |
|
Ожидаемые затраты на одного пациента после 10 циклов = 311 936 руб. ÷ 1000 пациентов |
312 |
||||
Тот же принцип используется для расчёта итоговой эффективности (например, сохранённых лет жизни (LYG)). Суммарное количество LYG рассчитывается исходя из количества живых пациентов в каждом из циклов, а далее полученное число делится на количество пациентов в модели. Средняя стоимость LYG рассчитывается путём деления стоимости LYG на количество лет.
Подобно модели Маркова, в дискретно-событийной модели (англ. discrete event simulation) пациенты находятся в одном и том же состоянии до появления определённых событий, например до изменения течения болезни, изменения тактики лечения, смерти. Находясь в определённом состоянии, пациенты могут иметь различные характеристики с течением времени и, следовательно, различные расходы на терапию, что обеспечивает большую гибкость модели, которая отсутствует при использовании модели Маркова [3].
_________
Источник: Включение лекарственных препаратов в ограничительные перечни: пошаговый алгоритм / под общ. ред. Белоусова Д. Ю., Зырянова С. К., Колбина А. С. — М. : Издательство ОКИ : Буки Веди, 2019. — 252 с. : ил. ISBN 978-5-4465-2555-3. https://clck.ru/MBP84
_________
Литература
- Куликов А. Ю., Нгуен Т. Т., Тихомирова А. В. Методология моделирования в фармакоэкономике [Электронный ресурс] // Фармакоэкономика. – 2011. – Т. 4. – № 4. – С. 8–16. – Режим доступа: https://clck.ru/FFnge
- Sullivan S. D., Mauskopf J. A., Augustovski F., et al. Principles of good practice for budget impact analysis II: Report of the ISPOR Task Force on Good Research Practices – Budget Impact Analysis [Электронный ресурс] // Value Health. – 2014. – № 17. – С. 5–14. – Режим доступа: https://clck.ru/HLDJ7
- Ягудина Р. И., Серпик В. Г. Методологические основы фармакоэкономического моделирования [Электронный ресурс] // Фармакоэкономика: теория и практика. – 2016. – Т. 4. – № 1. – С. 2–12. – Режим доступа: https://clck.ru/FFnh7
- Калашникова М. Ф., Белоусов Д. Ю., Чеберда А. Е., Фадеев В. В. Фармакоэкономический анализ применения современных пероральных сахароснижающих препаратов при недостаточном гликемическом контроле на метформине [Электронный ресурс] // Качественная клиническая практика. – 2019. – № 1. – С. 19–44. – Режим доступа: https://clck.ru/HXtXN
- Philips Z., Ginnelly L., Sculpher M., Claxton K., Golder S., Riemsma R., Woolacoot N., Glanville J. Review of guidelines for good practice in decision-analytic modelling in health technology assessment [Электронный ресурс] // Health Technol Assess. – 2004. – V. 8. – № 36. – Режим доступа: https://clck.ru/HXtdS
- Muennig P. Designing and Conducting Cost-Effectiveness Analysis in Medicine and Health Care [Электронный ресурс]. – San Francisco : Jossey-Bass, 2002. – Режим доступа: https://clck.ru/HXtF5
- Методические рекомендации по проведению сравнительной клинико-экономической оценки лекарственного препарата (новая редакция). Утверждены приказом ФГБУ «ЦЭККМП» Минздрава России от 29.12.2018 № 242-од [Электронный ресурс]. – Режим доступа: https://clck.ru/GqdJz
- Naimark D. M., Bott M., Krahn M. The half-cycle correction explained: two alternative pedagogical approaches [Электронный ресурс] // Med Decis Making. – 2008. – V. 28. – № 5. – С. 706–712. – Режим доступа: https://clck.ru/HXtbi
- Колбин А. С., Курылев А. А., Балыкина Ю. Е., Проскурин М. А., Насхлеташвили Д. Р. Клинико-экономическая оценка применения трастузумаба эмтазина у пациенток с HER2-положительным раком молочной железы с метастатическим поражением головного мозга [Электронный ресурс] // Качественная клиническая практика. – 2017. – № 2. – С. 4–11. – Режим доступа: https://clck.ru/HNhmd
.png)