Анализ чувствительности
- Методология /
-
8255
Анализ чувствительности (АЧ, англ. sensitive analysis (SA)) – это анализ, направленный на определение того, в какой степени будут меняться результаты исследования при изменениях исходных параметров.
Выбор параметров и уровень неопределённости для проведения АЧ необходимо обосновать. Проведение АЧ результатов расчётов к изменению исходных параметров в модели КЭА или АВБ можно применять к следующим параметрам:
- стоимости препаратов сравнения;
- стоимости медицинских услуг;
- показателям критериев эффективности (или полезности) и безопасности;
- колебаниям численности целевой популяции пациентов;
- временному горизонту (увеличивать, уменьшать вплоть до периода дожития).
Детерминированный анализ
Детерминированный анализ чувствительности (англ. deterministic sensitivity analysis) – это вид анализа, в котором исследователь самостоятельно выбирает список интересующих его параметров. При этом задаются различные значения одного или более параметров с определённым процентным отклонением от их исходной величины и наблюдаются изменения в полученных результатах.
Поскольку исследователь сам выбирает параметры и их альтернативные значения, включённые в детерминированный АЧ, то создаётся риск того, что его выбор будет предвзятым или нерациональным [1].
В случае детерминированного АЧ можно провести:
- однофакторный;
- многофакторный;
- пороговый.
Однофакторный АЧ (англ. one-way sensitivity analysis (OWSA)) – это вид анализа, в котором изучается влияние изменения одного параметра на результаты.
Результаты однофакторного АЧ могут быть представлены в виде диаграммы-торнадо (англ. Tornado Chart) – это гистограмма, где категории данных перечислены вертикально и упорядочены так, что наибольшая линия отображается в верхней части диаграммы, за ней следует второй по величине параметр и так далее вниз (рис. 1).
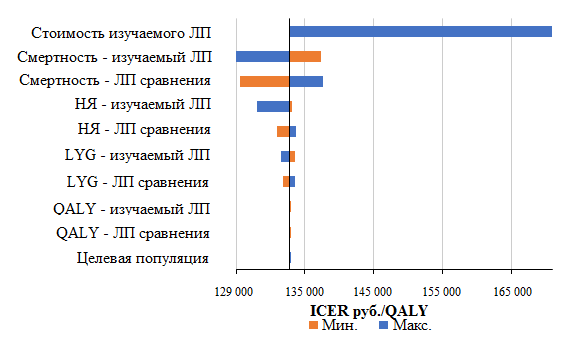
Рис. 1. Пример диаграммы-торнадо
Итоговый вид диаграммы визуально напоминает воронку торнадо, отсюда и название. Это один из основных способов визуализации результатов АЧ, полезный при сравнении относительной важности параметров, обладающих высокой степенью неопределённости, с другими, более стабильными параметрами. Для каждого рассматриваемого параметра вам понадобятся оценки того, какими будут минимальные, основные (вертикальная линия диаграммы-торнадо) и максимальные значения. В случае проведения однофакторного АЧ для анализа «затраты-эффективность» для построения диаграммы-торнадо вам потребуется:
- изменить значения стоимости препаратов сравнения или критерия эффективности;
- рассчитать изменённые показатели ICER;
- выделить минимальные и максимальные показатели ICER, полученные при изменении каждого интересующего параметра (затрат или эффективности);
- вычислить диапазон для каждого параметра;
- ранжировать параметры по убыванию диапазона разброса значений;
- построить график с «центром» в основном (базовом) значении ICER.
Более подробно узнать о методологии построения диаграммы-торнадо в MS Excel вы можете перейдя по ссылке clck.ru/HRNPi.
Многофакторный АЧ (англ. multivariate sensitivity analysis) – это вид анализа, в котором изучается одновременно влияние изменения нескольких параметров.
Поскольку возможно существование большого количества неопределённых параметров, то полный многофакторный АЧ может быть громоздким, сложным для понимания полученных результатов, поэтому наиболее часто он представляет собой анализ сценариев, дающий представление об эффективности ЛП в лучшем и худшем случае [1].
Пороговый АЧ (англ. threshold sensitivity analysis) – это вид детерминированного анализа, в котором сравниваются критические значения инкрементального показателя соотношения затрат и эффективности (ICER) с порогом готовности платить. В этом случае строят кривую приемлемости клинико-экономической эффективности (англ. cost-effectiveness acceptability curve (CEAC)). Данная кривая даёт графическое представление того, что ICER изучаемого ЛП является клинико-экономически приемлемым в пределах 95 % ДИ [2]. Перпендикулярные линии, опущенные из точек этой кривой, пересекают горизонтальную ось в точках, соответствующих значению ICER и границам его 95 % ДИ (рис. 2).
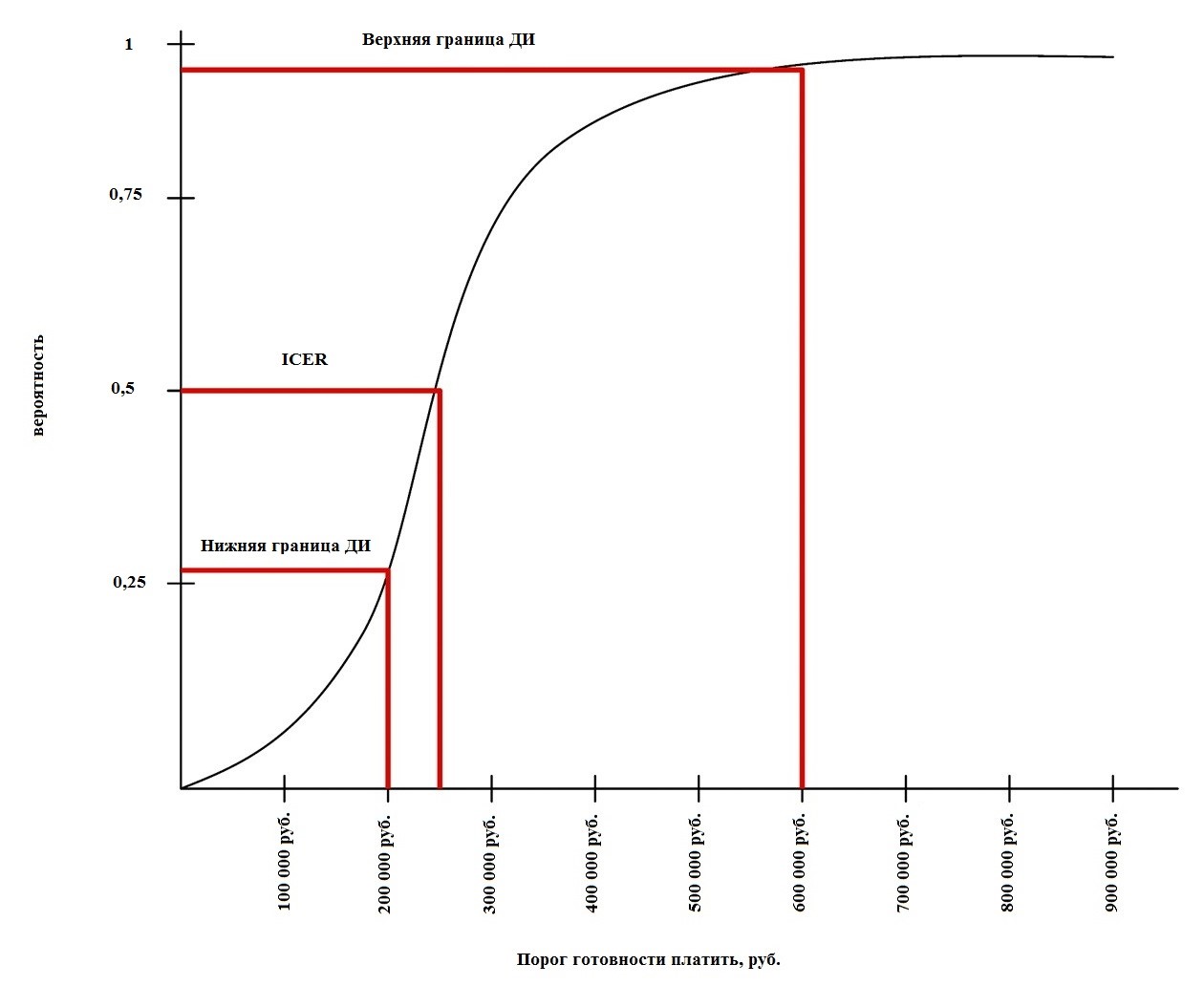
Рис. 2. Кривая приемлемости клинико-экономической эффективности
Вероятностный анализ чувствительности (англ. probabilistic sensitive analysis (PSA)) – это вид анализа, количественно измеряющий вероятность отклонения от расчётной величины изучаемого параметра.
Вероятностный АЧ можно провести с помощью симуляции Монте-Карло [3], основанной на получении большого числа повторений случайного (стохастического) процесса, который формируется таким образом, чтобы его вероятностные параметры оставались реалистичными: вероятность находится в пределах 0–1, а цена на ЛП не может быть отрицательной.
Монте-Карло симуляция (англ. Monte Carlo simulation) – это численный метод решения математических задач при помощи моделирования случайных величин.
Симуляция Монте-Карло относится к имитационному моделированию, в котором при расчёте какой-либо системы воспроизводится и исследуется поведение всех её компонентов, то есть из гипотетической когорты (приблизительно 104 человек) случайным образом выбирается пациент и проходит через модель (каждый пациент отдельно), что позволяет по исходным данным, содержащим сведения о начальном состоянии пациента, получить сведения о его состоянии на каждом последующем этапе. Модель запускается около 10 000 раз, а результат постоянно записывается, затем представляется вариация результатов в виде графика рассеяния эффективности затрат, где каждая симуляция отмечена на графике облаком точек и описывает дополнительные затраты и прирост эффективности анализируемого ЛП относительно препарата сравнения, основываясь на выборке входных параметров модели (рис. 3).
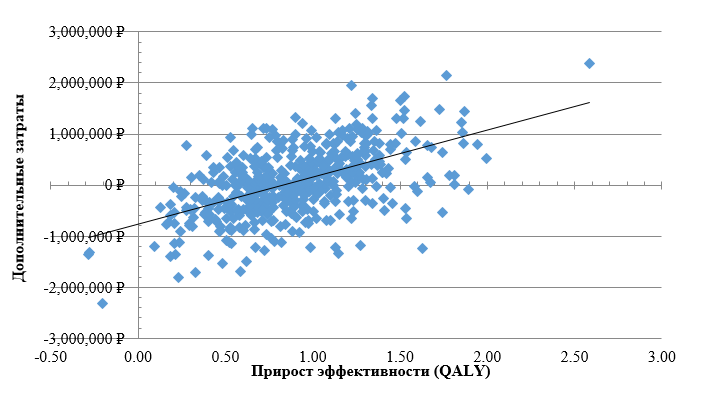
Рис. 3. График рассеяния эффективности затрат
Представление результатов анализа чувствительности
Однако, поскольку в официальных российских рекомендациях пока не описано, каким видом АЧ проводить проверку устойчивости полученных результатов КЭИ, не установлено официальное пороговое значение экономической целесообразности для ЛП, то представление результатов АЧ, рекомендуемое для подачи Предложения на включение ЛП в Перечни, отличается от описанного нами выше. В табл. 1 и 2 показаны примеры таблиц АЧ результатов расчётов к изменениям исходных параметров, требуемых Комиссией Минздрава РФ.
Таблица 1. Анализ чувствительности результатов расчётов к изменениям исходных параметров (изменяемый исходный параметр _________; значение параметра в анализе чувствительности _____________)
|
Показания к назначению |
Затраты на текущий вариант лекарственной терапии в АЧ, руб. |
Затраты на ожидаемый вариант лекарственной терапии в АЧ, руб. |
Разница затрат на лекарственную терапию в АЧ, руб. |
|
1. |
|
|
|
|
2. |
|
|
|
|
… |
|
|
|
Таблица 2. Анализ чувствительности результатов расчётов к изменениям исходных параметров (изменяемый исходный параметр _________; значение параметра в анализе чувствительности _____________)
|
Показания к назначению |
Прямые медицинские затраты на текущий вариант лекарственной терапии в АЧ, руб. |
Прямые медицинские затраты на ожидаемый вариант лекарственной терапии в АЧ, руб. |
Разница в прямых медицинских затратах в АЧ, руб. |
|
1. |
|
|
|
|
2. |
|
|
|
|
… |
|
|
|
_________
Источник: Включение лекарственных препаратов в ограничительные перечни: пошаговый алгоритм / под общ. ред. Белоусова Д. Ю., Зырянова С. К., Колбина А. С. — М. : Издательство ОКИ : Буки Веди, 2019. — 252 с. : ил. ISBN 978-5-4465-2555-3. https://clck.ru/MBP84
_________
Литература
- Ягудина Р. И., Куликов А. Ю., Новиков И. В. Современная методология анализа чувствительности в фармакоэкономических исследованиях [Электронный ресурс] // Фармакоэкономика. – 2010. – Т. 3. – № 4. – С. 8–12. – Режим доступа: https://clck.ru/HQfTo
- Симонов А. Н., Реброва О. Ю. Статистический анализ показателей клинико-экономической эффективности медицинских технологий [Электронный ресурс] // Медицинские технологии. Оценка и выбор. – 2015. – Т. 3. – № 21. – С. 8–14. – Режим доступа: https://clck.ru/HRZQ4
- Крысанов И. С. Имитационное моделирование на примере метода Монте-Карло симуляции [Электронный ресурс] // Фармакоэкономика. Современная фармакоэкономика и фармакоэпидемиология. – 2008. – № 2. – С. 3–5. – Режим доступа: https://clck.ru/FFnic
.png)